Determinantes sob um ponto de vista computacional:
Vamos considerar uma matriz A 25x25. Para obtermos det(A) poderiamos utilizar o Teorema de Laplace utilizando a expansão do cofator. Cada cofator Aij é o determinante de uma matriz 24x24 que pode ser expandida em relação a uma determinada linha ou coluna, requerendo 24 multiplicações. Desta forma, o cálculo de det(A) requer mais de 25! multiplicações. Mesmo se utilizassemos um computador capaz de fazer 10 trilhões de multiplicações por segundo, levariamos cerca de 49000 anos para calcular det(A).
Fonte: Livro "Introdução à Álgebra Linear com Aplicações"
domingo, 17 de maio de 2015
quinta-feira, 14 de maio de 2015
Teorema de Laplace
Teorema de Laplace:
Para entendermos o Teorema de Laplace é necessário entender o conceito básico de cofator (complemento algébrico).
Chamamos de cofator relativo a um elemento aij de uma matriz quadrada de ordem n, o número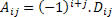
. Entendendo os elementos dessa expressão temos:
Aij: Cofator do elemento aij da matriz A;
Dij: Menor complementar, que nada mais é que o determinante da matriz A com a linha i e coluna j excluidas.
O Teorema de Laplace consiste em escolher uma linha/coluna e somar os produtos dos elemento dessa fila pelo seus respectivos cofatores. O resultado dessa soma será o determinante da matriz. O teorema pode ser melhor entendido com a seguinte ilustração:
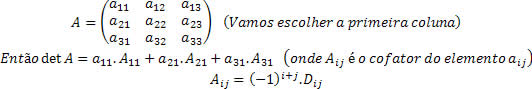
Exemplo:
Considerando a matiz C calcularemos seu determinante pelo Teorema de Laplace.
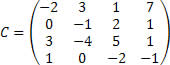
Vamos utilizar a primeira coluna para aplicar o Teorema.
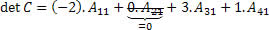
Fonte: imagem retirada do site Brasil escola.
Encontrando os valores dos cofatores de cada elemento temos:
.jpg)
.jpg)
Fonte: imagem retirada do site Brasil escola.
Somando os produtos de cada elemento pelo seu respectivo cofator temos o determinante da matriz C, conforme a seguinte expressão:
.jpg)
Fonte: imagem retirada do site Brasil escola.
Obs: Não foi necessário calcular o cofator do elemento a21, pois o elemento é nulo, deste modo o produto também será nulo.
Para entendermos o Teorema de Laplace é necessário entender o conceito básico de cofator (complemento algébrico).
Chamamos de cofator relativo a um elemento aij de uma matriz quadrada de ordem n, o número
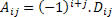. Entendendo os elementos dessa expressão temos:Aij: Cofator do elemento aij da matriz A;
Dij: Menor complementar, que nada mais é que o determinante da matriz A com a linha i e coluna j excluidas.
O Teorema de Laplace consiste em escolher uma linha/coluna e somar os produtos dos elemento dessa fila pelo seus respectivos cofatores. O resultado dessa soma será o determinante da matriz. O teorema pode ser melhor entendido com a seguinte ilustração:
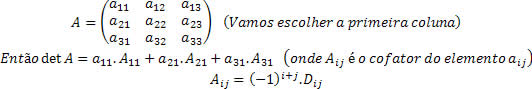
Fonte: imagem retirada do site Brasil escola.
Exemplo:
Considerando a matiz C calcularemos seu determinante pelo Teorema de Laplace.
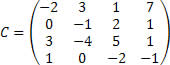
Fonte: imagem retirada do site Brasil escola.
Vamos utilizar a primeira coluna para aplicar o Teorema.
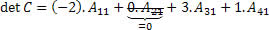
Fonte: imagem retirada do site Brasil escola.
Encontrando os valores dos cofatores de cada elemento temos:
Fonte: imagem retirada do site Brasil escola.
Somando os produtos de cada elemento pelo seu respectivo cofator temos o determinante da matriz C, conforme a seguinte expressão:
Fonte: imagem retirada do site Brasil escola.
Obs: Não foi necessário calcular o cofator do elemento a21, pois o elemento é nulo, deste modo o produto também será nulo.
Regra de Sarrus
Regra de Sarrus:
A ordem da matriz quadrada é que determina o melhor método para o cálculo de seu determinante. Para matrizes de ordem 2, por exemplo, basta calcular a diferença entre os produtos dos elementos da diagonal principal pelo produto dos elementos da diagonal secundária.
O matemático Pierre Frédéric Sarrus (1789-1861), nascido em Saint-Affrique, foi responsável pela regra prática de resolução de determinantes de ordem 3.
Para entendermos a Regra de Sarrus, vamos considerar a seguinte matriz A de ordem 3:
Fonte: imagem retirada do site Brasil escola.
O primeiro passo a ser tomado é copiar as duas primeiras colunas à direita da matriz A.
Fonte: imagem retirada do site Brasil escola.
Em seguida deve-se somar os produtos dos elementos da diagonal principal e das duas diagonais a direita da diagonal principal.
det Ap = a11.a22.a33 + a12.a23.a31 + a13.a21.a32
Fonte: imagem retirada do site Brasil escola.
O mesmo processo é realizado com a diagonal secundária e as duas diagonais a sua direita, porém, deve-se subtrair os produtos encontrados.
Fonte: imagem retirada do site Brasil escola.
Unindo os dois processos é possivel encontrar o determinante da matriz A, conforme o esquema abaixo:
Fonte: imagem retirada do site Brasil escola.
Exemplo:
Fonte: imagem retirada do site Brasil escola.
Dada a matriz B, calcularemos sua determinante pela Regra de Sarrus:
Fonte: imagem retirada do site Brasil escola.
A ordem da matriz quadrada é que determina o melhor método para o cálculo de seu determinante. Para matrizes de ordem 2, por exemplo, basta calcular a diferença entre os produtos dos elementos da diagonal principal pelo produto dos elementos da diagonal secundária.
O matemático Pierre Frédéric Sarrus (1789-1861), nascido em Saint-Affrique, foi responsável pela regra prática de resolução de determinantes de ordem 3.
Para entendermos a Regra de Sarrus, vamos considerar a seguinte matriz A de ordem 3:
Fonte: imagem retirada do site Brasil escola.
O primeiro passo a ser tomado é copiar as duas primeiras colunas à direita da matriz A.
Fonte: imagem retirada do site Brasil escola.
Em seguida deve-se somar os produtos dos elementos da diagonal principal e das duas diagonais a direita da diagonal principal.
det Ap = a11.a22.a33 + a12.a23.a31 + a13.a21.a32
Fonte: imagem retirada do site Brasil escola.
O mesmo processo é realizado com a diagonal secundária e as duas diagonais a sua direita, porém, deve-se subtrair os produtos encontrados.
det As = - a13.a22.31 - a11.a23.a32 - a12.a21.a33
Fonte: imagem retirada do site Brasil escola.
Unindo os dois processos é possivel encontrar o determinante da matriz A, conforme o esquema abaixo:
det A = det Ap + det As
det A = a11.a22.a33 + a12.a23.a31 + a13.a21.a32 - a13.a22.a31 - a11.a23.a32 - a12.a21.a33
Fonte: imagem retirada do site Brasil escola.
Exemplo:
Fonte: imagem retirada do site Brasil escola.
Dada a matriz B, calcularemos sua determinante pela Regra de Sarrus:
Fonte: imagem retirada do site Brasil escola.
det B = b11.b22.b33 + b12.b23.b31 + b13.b21.b32 - b13.b22.b31 - b11.b23.b32 - b12.b21.b33
det B = 1.3.2 + 5.0.4 + (-2).8.(-1) - (-2).3.4 - 1.0.(-1) - 5.8.2
det B = 6 + 0 + 16 - (-24) - 0 - 80
det B = 22 - 56
det B = - 34
terça-feira, 12 de maio de 2015
Regra de Chió
Regra de Chió
3. Calcular a matriz resultante e multiplicar o resultado por (−1) i+j , em que i e j são a linha e coluna do elemento igual a 1 escolhido inicialmente.
A Regra de Chió é um dispositivo prático
que serve para diminuir a ordem de uma
matriz sem alterar seu determinante. Ele é
consequência direta do Teorema de Laplace.
Para utilizá-lo, a matriz deve ter um
elemento aij = 1. Se a matriz não possuir um,
ele deve ser obtido usando o Teorema de Jacobi
Regra de Chió consiste em:
1. Eliminar da matriz a linha e coluna que
contém o elemento aij = 1.
Fonte:https://cursinhodapoliusp.files.wordpress.com/2012/07/material-determinantes.pdf
2. Subtrair dos elementos restantes, o produto
correspondentes na linha e coluna eliminadas.
Fonte:https://cursinhodapoliusp.files.wordpress.com/2012/07/material-determinantes.pdf
3. Calcular a matriz resultante e multiplicar o resultado por (−1) i+j , em que i e j são a linha e coluna do elemento igual a 1 escolhido inicialmente.
Fonte:https://cursinhodapoliusp.files.wordpress.com/2012/07/material-determinantes.pdf
Assim uma matriz 4x4 é transformada em uma 3x3 e podemos obter o determinante com maior facilidade aplicando outros métodos. Também é possível repetir a regra assim rebaixando a matriz ,tornando a uma 2x2.
fonte: https://cursinhodapoliusp.files.wordpress.com/2012/07/material-determinantes.pdf
Definição e Propriedades
Definição
Determinante é uma função que associa a cada matriz quadrada um número escalar.
Definimos determinante de A igual det(A) ou |A|.
Propriedades dos determinantes
1. O determinante de uma matriz A é igual ao determinante da sua transposta, então det(A)=det(At)
Demonstrando:
2. Se a matriz B é obtida da matriz A trocando-se posições duas linhas/colunas de A, então det(B)=-det(A)
Demonstrando:
3. Se duas linhas ou colunas de A são iguais, então det(A)=0
Demonstrando:
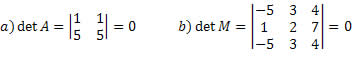
4. Se uma linha ou coluna de A é nula, então det(A)=0
Demonstrando:
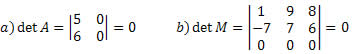
5. Se se os elementos acima ou abaixo forem iguais a zero, então o determinante da matriz será o produto dos elementos da diagonal principal.
Demonstrando:
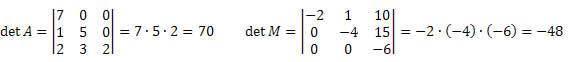
6. O determinante de um produto de duas matrizes é igual ao produto dos determinantes, isto é, det(AB)=det(A).det(B).
7. Se A é invertível, então det(A) diferente de zero.
Demonstrando:
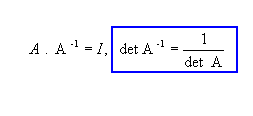
8. Se uma matriz A, quadrada de ordem m, for multiplicada por um número real p qualquer , então seu determinante será multiplicada por pm.
Demonstrando:
9. Se todos os elementos de uma linha ou coluna forem multiplicados por um número real p qualquer , seu determinante também será multiplicado por p.
Demonstrando:
10. Teorema de Jacobi: o determinante de uma matriz não se altera quando somamos aos elementos de uma fila uma combinação linear dos elementos correspondentes de filas paralelas.
Demonstrando:
dado
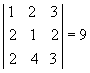
substituindo a 1º coluna pela soma dessa com o dobro da segunda, obteremos
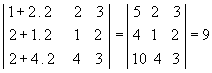
*Referências: http://www.alunosonline.com.br/matematica/propriedades-dos-determinantes.html
http://www.somatematica.com.br/emedio/determinantes/determinantes4.php
Definimos determinante de A igual det(A) ou |A|.
Propriedades dos determinantes
1. O determinante de uma matriz A é igual ao determinante da sua transposta, então det(A)=det(At)
Demonstrando:
Fonte: imagem retirada do site alunos online
2. Se a matriz B é obtida da matriz A trocando-se posições duas linhas/colunas de A, então det(B)=-det(A)
Demonstrando:
Fonte: imagem retirada do site alunos online
3. Se duas linhas ou colunas de A são iguais, então det(A)=0
Demonstrando:
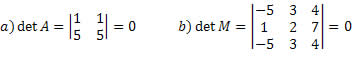
Fonte: imagem retirada do site alunos online
4. Se uma linha ou coluna de A é nula, então det(A)=0
Demonstrando:
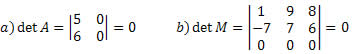
Fonte: imagem retirada do site alunos online
5. Se se os elementos acima ou abaixo forem iguais a zero, então o determinante da matriz será o produto dos elementos da diagonal principal.
Demonstrando:
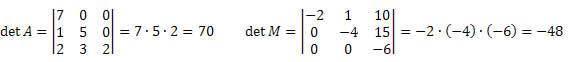
Fonte: imagem retirada do site alunos online
6. O determinante de um produto de duas matrizes é igual ao produto dos determinantes, isto é, det(AB)=det(A).det(B).
7. Se A é invertível, então det(A) diferente de zero.
Demonstrando:
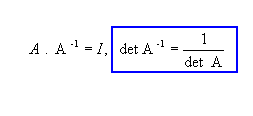
Fonte: imagem retirada do site só matemática.
8. Se uma matriz A, quadrada de ordem m, for multiplicada por um número real p qualquer , então seu determinante será multiplicada por pm.
det (p∙A) = pm∙det A
Demonstrando:
Fonte: imagem retirada do site alunos online
9. Se todos os elementos de uma linha ou coluna forem multiplicados por um número real p qualquer , seu determinante também será multiplicado por p.
Demonstrando:
Fonte: imagem retirada do site alunos online
10. Teorema de Jacobi: o determinante de uma matriz não se altera quando somamos aos elementos de uma fila uma combinação linear dos elementos correspondentes de filas paralelas.
Demonstrando:
dado
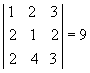
Fonte: imagem retirada do site só matemática.
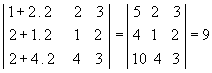
Fonte: imagem retirada do site só matemática.
*Referências: http://www.alunosonline.com.br/matematica/propriedades-dos-determinantes.html
http://www.somatematica.com.br/emedio/determinantes/determinantes4.php
Assinar:
Postagens (Atom)