Determinante é uma função que associa a cada matriz quadrada um número escalar.
Definimos determinante de A igual det(A) ou |A|.
Propriedades dos determinantes
1. O determinante de uma matriz A é igual ao determinante da sua transposta, então det(A)=det(At)
Demonstrando:

2. Se a matriz B é obtida da matriz A trocando-se posições duas linhas/colunas de A, então det(B)=-det(A)
Demonstrando:

3. Se duas linhas ou colunas de A são iguais, então det(A)=0
Demonstrando:
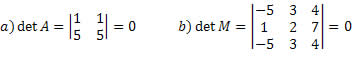
4. Se uma linha ou coluna de A é nula, então det(A)=0
Demonstrando:
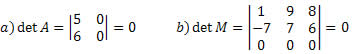
5. Se se os elementos acima ou abaixo forem iguais a zero, então o determinante da matriz será o produto dos elementos da diagonal principal.
Demonstrando:
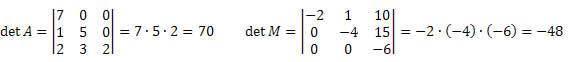
6. O determinante de um produto de duas matrizes é igual ao produto dos determinantes, isto é, det(AB)=det(A).det(B).
7. Se A é invertível, então det(A) diferente de zero.
Demonstrando:
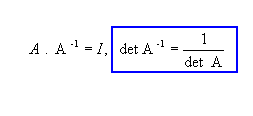
8. Se uma matriz A, quadrada de ordem m, for multiplicada por um número real p qualquer , então seu determinante será multiplicada por pm.
Demonstrando:

9. Se todos os elementos de uma linha ou coluna forem multiplicados por um número real p qualquer , seu determinante também será multiplicado por p.
Demonstrando:

10. Teorema de Jacobi: o determinante de uma matriz não se altera quando somamos aos elementos de uma fila uma combinação linear dos elementos correspondentes de filas paralelas.
Demonstrando:
dado
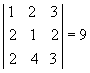
substituindo a 1º coluna pela soma dessa com o dobro da segunda, obteremos
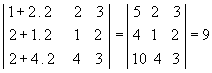
*Referências: http://www.alunosonline.com.br/matematica/propriedades-dos-determinantes.html
http://www.somatematica.com.br/emedio/determinantes/determinantes4.php
Definimos determinante de A igual det(A) ou |A|.
Propriedades dos determinantes
1. O determinante de uma matriz A é igual ao determinante da sua transposta, então det(A)=det(At)
Demonstrando:

Fonte: imagem retirada do site alunos online
2. Se a matriz B é obtida da matriz A trocando-se posições duas linhas/colunas de A, então det(B)=-det(A)
Demonstrando:

Fonte: imagem retirada do site alunos online
3. Se duas linhas ou colunas de A são iguais, então det(A)=0
Demonstrando:
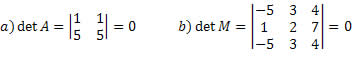
Fonte: imagem retirada do site alunos online
4. Se uma linha ou coluna de A é nula, então det(A)=0
Demonstrando:
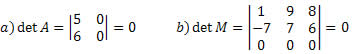
Fonte: imagem retirada do site alunos online
5. Se se os elementos acima ou abaixo forem iguais a zero, então o determinante da matriz será o produto dos elementos da diagonal principal.
Demonstrando:
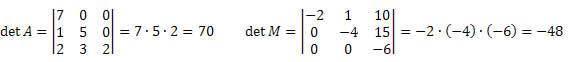
Fonte: imagem retirada do site alunos online
6. O determinante de um produto de duas matrizes é igual ao produto dos determinantes, isto é, det(AB)=det(A).det(B).
7. Se A é invertível, então det(A) diferente de zero.
Demonstrando:
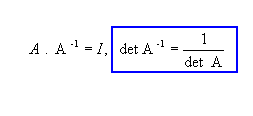
Fonte: imagem retirada do site só matemática.
8. Se uma matriz A, quadrada de ordem m, for multiplicada por um número real p qualquer , então seu determinante será multiplicada por pm.
det (p∙A) = pm∙det A
Demonstrando:

Fonte: imagem retirada do site alunos online
9. Se todos os elementos de uma linha ou coluna forem multiplicados por um número real p qualquer , seu determinante também será multiplicado por p.
Demonstrando:

Fonte: imagem retirada do site alunos online
10. Teorema de Jacobi: o determinante de uma matriz não se altera quando somamos aos elementos de uma fila uma combinação linear dos elementos correspondentes de filas paralelas.
Demonstrando:
dado
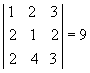
Fonte: imagem retirada do site só matemática.
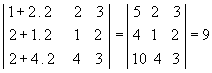
Fonte: imagem retirada do site só matemática.
*Referências: http://www.alunosonline.com.br/matematica/propriedades-dos-determinantes.html
http://www.somatematica.com.br/emedio/determinantes/determinantes4.php
Nenhum comentário:
Postar um comentário