Teorema de Laplace

Teorema de Laplace:

          Para entendermos o Teorema de Laplace é necessário entender o conceito básico de cofator (complemento algébrico).
          Chamamos de cofator relativo a um elemento aij de uma matriz quadrada de ordem n, o número 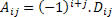. Entendendo os elementos dessa expressão temos:

Aij: Cofator do elemento aij da matriz A;
Dij: Menor complementar, que nada mais é que o determinante da matriz A com a linha i e coluna j excluidas.

          O Teorema de Laplace consiste em escolher uma linha/coluna e somar os produtos dos elemento dessa fila pelo seus respectivos cofatores. O resultado dessa soma será o determinante da matriz. O teorema pode ser melhor entendido com a seguinte ilustração:



 

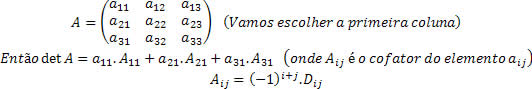
                                                        Fonte: imagem retirada do site Brasil escola.

Exemplo:

          Considerando a matiz C calcularemos seu determinante pelo Teorema de Laplace.

                                                

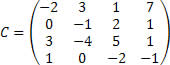
                                                       Fonte: imagem retirada do site Brasil escola.

          Vamos utilizar a primeira coluna para aplicar o Teorema.

                                   

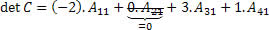
                                                        Fonte: imagem retirada do site Brasil escola.

          Encontrando os valores dos cofatores de cada elemento temos:

                       

                       

                       

                                                           Fonte: imagem retirada do site Brasil escola.

          Somando os produtos de cada elemento pelo seu respectivo cofator temos o determinante da matriz C, conforme a seguinte expressão:

                             

                                                              Fonte: imagem retirada do site Brasil escola.

          Obs: Não foi necessário calcular o cofator do elemento a21, pois o elemento é nulo, deste modo o produto também será nulo.